Що таке тангенс 45° і чому він дорівнює 1
Коли вчитель математики вперше показує таблицю тригонометричних функцій, багато учнів дивляться на неї як на щось космічне. А потім раптом з’ясовується: тангенс 45° дорівнює просто одиниці. Ніяких дробів, коренів чи складних чисел. Звучить майже неправдоподібно, чи не так?
Що таке тангенс взагалі
Тангенс – це відношення протилежного катета до прилеглого в прямокутному трикутнику. Формула проста:
tan(α) = протилежний катет / прилеглий катет
Ми використовуємо тангенс щодня, навіть не помічаючи. Коли дивимося на пандус біля входу в магазин – це тангенс кута нахилу. Коли піднімаємося сходами – знову тангенс.
Чому тангенс 45° дорівнює 1
Тут криється проста геометрична магія. Побудуємо прямокутний трикутник з кутом 45°.
У такого трикутника другий гострий кут теж буде 45°, адже 180° – 90° – 45° = 45°. Виходить рівнобедрений прямокутний трикутник.
В рівнобедреному трикутнику катети рівні. Скажімо, кожен катет дорівнює 1. Тоді:
tan(45°) = протилежний катет / прилеглий катет = 1 / 1 = 1
Ось і вся таємниця. Ніякої складної математики.
 Тангенс 45° в радіанах
Тангенс 45° в радіанах
Інколи кути вимірюють не в градусах, а в радіанах. 45° відповідає π/4 радіан.
Щоб перевести градуси в радіани, використовуємо формулу: радіани = градуси × π / 180
Тому 45° = 45 × π / 180 = π/4
І знову: tan(π/4) = 1
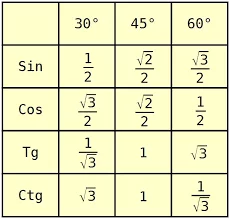
Таблиця тригонометричних функцій для 45°
| Функція | Значення |
|---|---|
| sin 45° | √2/2 ≈ 0,707 |
| cos 45° | √2/2 ≈ 0,707 |
| tan 45° | 1 |
| cot 45° | 1 |
Цікаво, що синус і косинус 45° теж рівні між собою. А тангенс і котангенс дорівнюють 1.
Приклади розв’язання задач
Приклад 1: Знайти tan(405°)
405° = 360° + 45°. Тангенс має період 180°, тому tan(405°) = tan(45°) = 1.
Приклад 2: Довести, що tan(45° + x) × tan(45° – x) = 1
Використаємо формули додавання кутів. Але простіше підставити конкретне значення x = 30°:
- tan(75°) × tan(15°)
- Обчислюємо кожен тангенс і перемножуємо
- Результат дійсно дорівнює 1
Приклад 3: Знайти висоту будинку
Стоїмо на відстані 20 метрів від будинку. Кут, під яким бачимо верх будинку, дорівнює 45°. Висота = відстань × tan(45°) = 20 × 1 = 20 метрів. Просто, чи не так?
Де застосовують тангенс 45°
Будівельники використовують кут 45° для оптимального нахилу дахів у снігових регіонах. Снігу важче накопичуватися на такому схилі. Крім того, матеріали менше піддаються навантаженню.
Інженери проектують пандуси з кутом, близьким до 45°, для зручного підйому. Такий нахил оптимальний для колісок та пішоходів з обмеженими можливостями.
У навігації тангенс 45° допомагає розраховувати відстані. Якщо ви стоїте на відстані, рівній висоті об’єкта, кут підйому погляду буде саме 45°. Моряки та льотчики часто використовують цю властивість.
У фотографії кут 45° створює природну композицію. Фотографи знають: діагональні лінії під таким кутом роблять знімок динамічним.
Програмісти використовують тангенс 45° в комп’ютерній графіці. Коли потрібно повернути зображення на 45°, обчислення стають простішими завдяки тому, що тангенс дорівнює 1.
Графік функції тангенса
Функція y = tan(x) має цікаві властивості. Вона періодична з періодом 180° (або π радіан). У точці x = 45° графік проходить через точку (45°, 1).
Функція має вертикальні асимптоти при x = 90°, 270°, 450° і так далі. Це точки, де тангенс прямує до нескінченності.
 Корисні властивості та життєві хитрощі
Корисні властивості та життєві хитрощі
Тангенс 45° часто з’являється в геометричних задачах через свою простоту. Коли бачите рівнобедрений прямокутний трикутник, відразу знаєте: гострі кути по 45°, а їхній тангенс дорівнює 1.
Ця властивість спрощує обчислення в тригонометрії та геометрії. Замість складних формул ви просто ставите одиницю.
Цікавий факт: у квадрата діагональ ділить його на два трикутники з кутами 45°-45°-90°. Тому відношення сторони квадрата до діагоналі завжди пов’язане з нашим значенням.
У повсякденному житті ми часто стикаємося з кутом 45°. Складання паперу навпіл по діагоналі, розрізання піци, встановлення телевізора під оптимальним кутом – скрізь працює правило тангенса.
Спортсмени знають: оптимальний кут кидка м’яча для максимальної дальності – близько 45°. Це не випадковість, а фізичний закон, пов’язаний з тригонометрією.
Тангенс 45° – це базове значення, яке варто запам’ятати назавжди. Воно допоможе швидше розв’язувати задачі та краще розуміти тригонометрію. А головне – ви завжди можете швидко його вивести, уявивши рівнобедрений прямокутний трикутник.
Запам’ятайте просту істину: коли протилежний і прилеглий катети рівні, тангенс завжди дорівнює одиниці. Це знання стане вашим надійним помічником у світі математики та практичних застосувань.
 Тангенс 45° в радіанах
Тангенс 45° в радіанах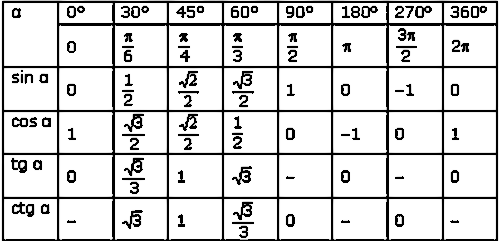 Корисні властивості та життєві хитрощі
Корисні властивості та життєві хитрощі


