Властивості степенів: простими словами про головні правила математики
Якщо колись у школі вас бентежили вирази на кшталт a3×a4a^3 \times a^4 або (a2)3(a^2)^3, ви не самі. Степені здаються складними лише доти, доки не зрозумієш їхню логіку. Насправді це — зручний інструмент, який допомагає скорочувати записи, обчислювати великі числа й бачити закономірності. Трохи уваги — і все стає на свої місця.
Що таке степінь і навіщо він потрібен
Степінь — це скорочений спосіб запису множення однакових чисел. Наприклад, 343^4 означає 3×3×3×33 \times 3 \times 3 \times 3. Але за цим записом стоїть більше, ніж просто множення. Степені описують ріст — від збільшення площі до піднесення потужності комп’ютера чи обсягу даних.
Приклад із життя: якщо кожного дня ви подвоюєте кількість сторінок, які читаєте, через тиждень прочитаєте не 14, а 27=1282^7 = 128 сторінок. Це і є сила степеня — показувати, як швидко все зростає.
М’який заклик: звертайте увагу на закономірності — вони допомагають не зазубрювати, а розуміти.
Основні властивості степенів, які варто запам’ятати
Добуток степенів з однаковими основами
Якщо основа одна, показники додаються:
am×an=am+na^m \times a^n = a^{m+n}
 Приклад: 23×24=23+4=272^3 \times 2^4 = 2^{3+4} = 2^7.
Приклад: 23×24=23+4=272^3 \times 2^4 = 2^{3+4} = 2^7.
Це правило часто використовують у фізиці чи економіці, коли треба швидко порахувати зростання показників.
Частка степенів з однаковими основами
Коли ділимо степені з однаковою основою, показники віднімаються:
am:an=am−na^m : a^n = a^{m-n}
Приклад: 56:52=56−2=545^6 : 5^2 = 5^{6-2} = 5^4.
Так легко спростити великі вирази або зробити обчислення без калькулятора.
Степінь від степеня
Коли підносимо степінь до степеня — показники множимо:
(am)n=am×n(a^m)^n = a^{m \times n}
Приклад: (32)3=36(3^2)^3 = 3^{6}.
Це допомагає скоротити довгі обчислення у формулах, особливо під час підготовки до ЗНО.
Добуток у степені
Якщо в дужках стоїть добуток, то кожен множник підноситься окремо:
(ab)n=an×bn(ab)^n = a^n \times b^n
Приклад: (2×3)4=24×34(2 \times 3)^4 = 2^4 \times 3^4.
Це властивість показує, що степені розподіляються по множниках.
Частка у степені
Те саме працює і для ділення:
(ab)n=anbn\left( \frac{a}{b} \right)^n = \frac{a^n}{b^n}
Приклад: (6/2)3=63/23=27(6/2)^3 = 6^3 / 2^3 = 27.
Просте правило, яке допомагає не заплутатись у дробах.
Нульовий і від’ємний показники
a0=1a^0 = 1 (для будь-якого числа, окрім нуля).
a−n=1ana^{-n} = \frac{1}{a^n}.
Приклад: 4−2=1/42=1/164^{-2} = 1/4^2 = 1/16.
Такі степені часто плутають, але це просто інша форма запису дробу.
М’який заклик: не поспішайте запам’ятовувати. Зрозумійте суть — і формули стануть логічними.
Як запам’ятати властивості степенів назавжди
Щоб не плутатися, зручно користуватись асоціаціями:
Додавання показників — коли числа ростуть разом.
Віднімання — коли одне зменшує інше.
Множення показників — як багаторазове повторення дії.
Можна навіть зробити невеличку таблицю для швидкого повторення:
| Дія | Формула | Приклад |
|---|---|---|
| Добуток | am×an=am+na^m \times a^n = a^{m+n} | 22×23=252^2 \times 2^3 = 2^5 |
| Частка | am:an=am−na^m : a^n = a^{m-n} | 35:32=333^5 : 3^2 = 3^3 |
| Степінь від степеня | (am)n=amn(a^m)^n = a^{mn} | (52)3=56(5^2)^3 = 5^6 |
Де в житті зустрічаються степені
Ми постійно стикаємося зі степенями, навіть не думаючи про це.
Технології: збільшення пам’яті комп’ютера — це подвоєння, тобто 2n2^n.
Біологія: ріст бактерій чи клітин відбувається за експоненційним законом.
Фінанси: відсотки за депозитом теж працюють «у степені».
Цитата:
Математика не про числа, а про логіку, яка стоїть за ними.
М’який заклик: спостерігайте, як степені проявляються у вашому житті — тоді формули оживають.
 Типові помилки при роботі зі степенями
Типові помилки при роботі зі степенями
Додавання основ замість показників.
Наприклад, 23+23≠262^3 + 2^3 \neq 2^6. Це просто 8+8=168 + 8 = 16.Ігнорування нульового степеня.
Будь-яке число в нульовому степені — одиниця, а не нуль.Неправильне застосування від’ємного показника.
a−2a^{-2} — це не мінус, а обернене значення.
Цитата:
Помилка — це ще одна форма навчання. Головне — зрозуміти, де і чому вона виникла.
Властивості степенів — це не набір сухих правил, а логіка, яка пронизує світ чисел. Розібравшись із нею, ви зможете легко спрощувати вирази, рахувати в голові й навіть краще розуміти природні процеси.
Математика — це не лише формули, а спосіб мислення. Варто одного разу відчути цю логіку — і все стане простим.
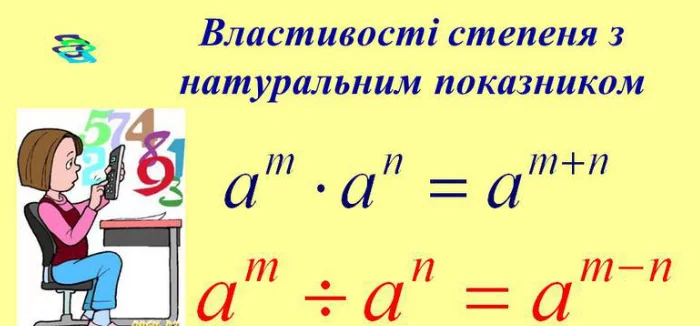 Типові помилки при роботі зі степенями
Типові помилки при роботі зі степенями


