Як віднімати дроби з різними знаменниками: покрокова інструкція
Якщо ви коли-небудь стикалися з дробами в школі, то напевно знаєте, як непросто зрозуміти, як з ними працювати. Одне з найбільш важливих і водночас складних завдань — це віднімання дробів з різними знаменниками. Але не переживайте, зараз ми розберемо це на прикладах, і все стане набагато зрозуміліше.
Що таке дроби з різними знаменниками?
Перед тим як віднімати дроби з різними знаменниками, давайте згадаємо, що саме ми маємо на увазі. Дроби складаються з двох частин: чисельника і знаменника. Наприклад, у дробі 3/4, 3 — це чисельник, а 4 — знаменник. Коли дроби мають різні знаменники, їх складно віднімати без попередньої обробки.
Уявіть собі ситуацію: у вас є дві пари шкарпеток, але одна пара з трьох і одна — з п’яти. Як їх порівняти або відняти одну від іншої? Логічно, для того щоб вони були порівнянними, потрібно обидві пари перевести в однаковий розмір. З дробами працює точно так само — для того щоб відняти їх, потрібно привести їх до спільного знаменника.
Зведення дробів до спільного знаменника
Перший крок до віднімання дробів з різними знаменниками — це зведення їх до спільного знаменника. Найлегше це зробити, знайшовши найменший спільний знаменник (НСК) для обох дробів.
Як це працює на практиці? Розглянемо приклад дробів 1/4 і 1/6. Спочатку знаходимо НСК для 4 і 6. Для цього потрібно розкласти числа на прості множники:
4 = 2 * 2
6 = 2 * 3
НСК буде 12, бо це найменше число, яке ділиться на 4 і на 6.
Тепер зводимо кожен дріб до знаменника 12:
1/4 = 3/12
1/6 = 2/12
Отже, ми тепер можемо легко відняти ці дроби.
 Алгоритм віднімання дробів з різними знаменниками
Алгоритм віднімання дробів з різними знаменниками
Знайдіть найменший спільний знаменник (НСК) для двох дробів. Якщо знаменники чисел не взаємно прості, то НСК буде добутком цих чисел.
Зведіть дроби до спільного знаменника. Для цього потрібно кожен дріб помножити чисельник і знаменник на таке число, щоб знаменник став рівним НСК.
Відніміть чисельники. Після того як ви привели дроби до спільного знаменника, просто відніміть чисельники один від одного.
Скоротіть дріб. Після віднімання дробів може бути доцільно скоротити результат.
Приклад: 3/4 – 2/5
Давайте розглянемо приклад на конкретному числовому прикладі. Ми будемо віднімати дроби 3/4 і 2/5.
Знайдемо НСК для 4 і 5. Оскільки ці числа взаємно прості, НСК буде 20.
Тепер зводимо дроби до знаменника 20:
3/4 = 15/20 (тут чисельник множиться на 5)
2/5 = 8/20 (тут чисельник множиться на 4)
Тепер віднімаємо чисельники: 15 – 8 = 7. Отже, результат буде 7/20.
Ми отримали результат 7/20, який вже не можна скоротити, тому це й буде остаточний результат.
 Поширені помилки та як їх уникнути
Поширені помилки та як їх уникнути
Багато учнів роблять кілька типових помилок при відніманні дробів з різними знаменниками. Ось декілька з них:
Не знаходять НСК. Це одна з найбільш поширених помилок, адже без спільного знаменника дроби неможливо порівняти або відняти. Завжди перевіряйте знаменники!
Помилка при зведенні дробів до спільного знаменника. Пам’ятайте, що потрібно множити і чисельник, і знаменник на потрібне число. Якщо помножите тільки знаменник, результат буде неправильною дробью.
Не скорочують результат. Після того, як ви відняли дроби, не забувайте перевіряти, чи можна скоротити отриману відповідь.
Заклик до дії
Якщо ви ще не спробували віднімати дроби з різними знаменниками, обов’язково спробуйте на простих прикладах. Практика — найкращий спосіб закріпити матеріал. Чим більше прикладів ви розв’яжете, тим впевненіше будете себе почувати у цьому процесі.
Віднімання дробів з різними знаменниками може здатися складним на перший погляд, але як тільки ви зрозумієте принцип зведення дробів до спільного знаменника, цей процес стане для вас простим і зрозумілим. Дроби — це не тільки теоретичний матеріал, а й корисний інструмент, який ви будете використовувати не лише в школі, а й у повсякденному житті, навіть якщо цього не помічаєте.
Тож не бійтеся дробів, і дайте собі час на тренування. Як і в будь-якому іншому завданні, регулярні вправи допоможуть вам досягти майстерності!
 Алгоритм віднімання дробів з різними знаменниками
Алгоритм віднімання дробів з різними знаменниками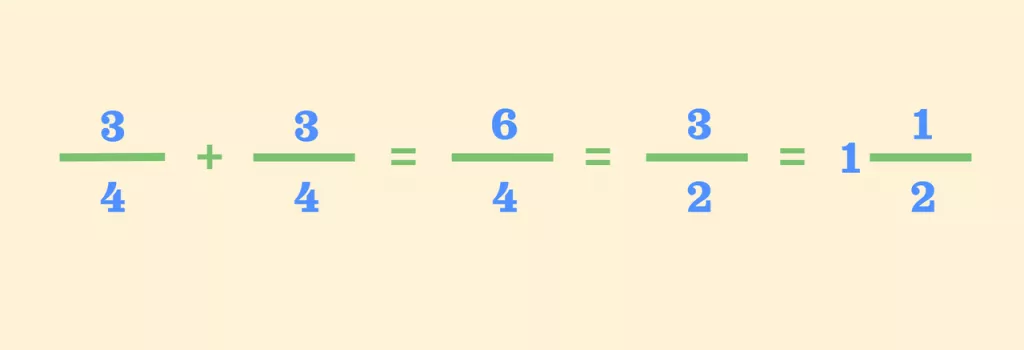 Поширені помилки та як їх уникнути
Поширені помилки та як їх уникнути


